Discuss the influence of linguistic and cultural factors on number processing
The acquisition of numerical systems and the subsequent mathematical applications of these can be seen as one of humanity’s greatest achievements. Numbers allow us to record observations, explain natural phenomena and develop advanced technologies. Mathematics is the only field in which perfect, indisputable proof can be obtained. Darwinian evolution could be false, reality could be an illusion but, a2 + b2 will always equal c2.
The earliest evidence of number use was that of a tally system inscribed on a fossilised wolf’s bone 30,000 years ago (Weiese, 2007). Various numeral systems have been developed throughout history. The most common system used today is the decimal system (base-ten). However, the remnants of now defunct numeral systems can still be found. The sexagesimal system (base-sixty), refined in ancient Babylonia, is the basis for modern representation of both time and angle measurement. The Babylonians could count up to 60 on their hands using a combination the 12 knuckles on the right hand and the five digits on the left hand (Du Sautoy, 2010).
The examination of numerical processing between cultures is best implemented through a common paradigm. Dehaene’s Triple Code Model (1992, Fig i) (TCM) is an influential theory of numerical processing that provides a universal framework to encapsulate numerical processes. The model divides number processing into three areas:
The analogue magnitude representation (AMR) gives us the semantic quantity of the number and in turn allows for approximate calculation, comparison and subitizing (instant recognition of small quantities). This code is the preverbal system of arithmetic reasoning and has been observed universally in infants and animals.
The verbal word frame (VWF) is the oral representation of number, e.g. “Seven” in English or “Hohk” in Thai. This code is part of the language processing system and enables the labelling and storage of number words and in turn, the counting process.
The visual number form (VNF) is the written representation of number, e.g. “7” in Arabic numerals, or “๗” in Thai numerals. This allows numbers to be represented in an efficient manner (as opposed to tallying), parity to be deduced and multi-digit operations to be calculated.
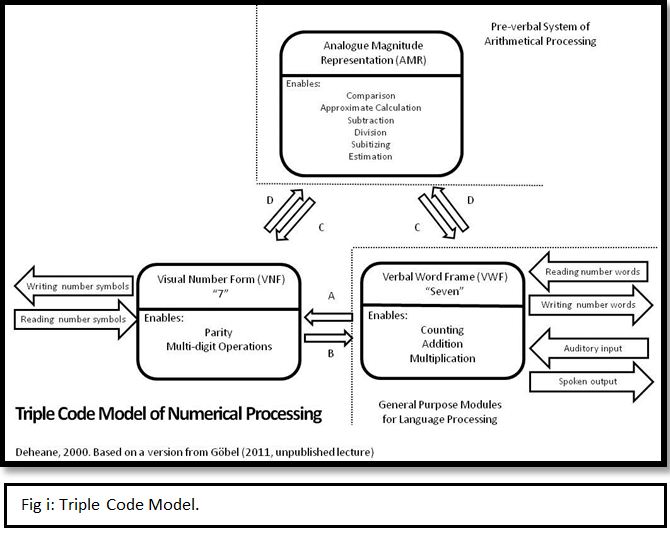
These three codes work in conjunction to facilitate the three stages of numerical processing; perception of various number representations (interpretation of a mathematical “problem”), the transformation of number (mental arithmetic) and the output of number (oral/written “answer”). Using the TCM, an examination of the effect of language and culture on numerical processing can be split into two distinct categories of study; comparison of cultures whereby numerical concepts differ only in labelling (i.e. the difference between the English “Twenty-Two” and the German “Zweiundzwanzig”) and comparison of cultures whereby different numerical systems are used. For example, the use of the decimal system contrasted with the Anindilyakwa tribe’s use of a quinary (base-five) system.
Most cultures that do not use the decimal system are those tribal societies that have not been influenced by modernity. These cultures will be examined first. The decimal system is structured in such a way that cardinal numbers follow a systematic rule which can attribute a label and place order to any quantity. However, a number of tribal communities lack a consistent system to enable counting words (CWs) to ascend infinitely. It follows that if these cultures lack a VWF for given quantities, they also lack a VNF and without these, will be only be able to count or perform addition and multiplication with numbers for which there are CWs. They should however, using the AMR, be able to estimate, compare and approximate calculations for numbers larger than those for which they possess CWs.
The Pirahã people of the Amazon have no CWs for cardinal numbers and are unique in that their language is the only living tongue studied which has no exact morpheme for “one” (Frank, Everett, Fedorenko & Gibson, 2008). Instead they have three CWs which denote various approximate quantities; “hói” (roughly one, up to six), “hoí” (few) and “baagiso” (many). Frank et al. (2008) found that although the Pirahã could replicate exact numerosities in open-matching tasks (copying an array of six objects) they were unable to replicate quantities in tasks where memory was needed to encode and reproduce an exact quantity (reproducing the number of balls dropped into a tin-can). This is consistent with the TCM’s observation that without a VWF for exact CWs, representations of exact quantity cannot be remembered and reproduced.
Frank et al. (2008) conclude that the success rate of the open-matching task indicates the Pirahã “were able to appreciate the necessity of matching the quantity of objects exactly” (pp. 823), and that they recognised that “one item more or less… is not a correct response” (pp. 824). However, this implies that the participants had an idea of “oneness” and given that they do not have a lexical marker for this most basic assumption of number, it seems unlikely they would appreciate its numerical importance to the quantity of a set. Instead, I propose that the Pirahã completed the task using a spatial strategy to copy the shape and pattern of the array with no thought towards any notion of exact quantity.
Pica et al. (2004) studied another Amazonian tribe, the Mundurukú. Their language has CWs for numbers one to five and other approximate terms such as “many” and “a small quantity”. However, CWs were used only exactly for the terms “one” and “two” while all other CWs were used inconsistently for a range of numbers. A number of experiments were conducted using printed dots on paper to represent quantities. During these tests (comparison of items, approximate addition and exact subtraction) the Mundurukú were unable to exactly calculate numbers above five. Some experiments did show they could compare and perform approximate arithmetic of numbers much larger than those for which they had CWs. These findings concur with the TCM; exact calculation was possible, but only for numbers which could be encoded through the VWF (i.e. those with CWs). Any quantity without a CW could only be processed within the AMR and therefore could only be estimated approximately.
A number of indigenous Australian communities have only a limited set of CWs. Butterworth, Reeve, Reynolds & Lloyd (2008) sought to determine how this lack of CWs affected indigenous children’s mathematical skills. Two Australian aboriginal tribes were studied; the Walipiri and the Anindilyakwa. The Walipiri have three CWs; jinta (singular), jirrama (dual plural) and marnkurrpa (greater than dual plural). These CWs have synonyms but the three types of number remain constant. The Anindilyakwa have a more complex system which has CWs for “one”, “two”, “three” and “more than three” as well as a quinary numeral system that is not introduced until adolescence. This system is only computed by the elders of the society who use it infrequently for special cultural events (i.e. distribution of eggs). The children in this study have no knowledge of the system.
Groups of children from both tribes and from an English speaking community participated in four experiments to determine their mathematical ability. First, children were shown a number of counters that were then hidden and the children had to reproduce the same number of counters. In the second task, cross-modal matching, children heard two wooden blocks being tapped together. They then had to produce the same number of counters as the taps they had heard. For the third task, non-verbal addition, the children were shown a set of counters. These counters were then hidden under a mat before additional counters were slid underneath. The children then had to replicate the number of counters under the mat. The fourth task, division, asked children to share objects between teddy-bears. During all the experiments, it was observed that language did not seem to have any effect and the performance of all the children was similar. One variable that did influence task performance was age; older children in all groups performed better than their younger counterparts.
The TCM can readily explain the execution of division without CWs as this process takes place within the AMR. It is worth noting that this form of division can only take place with the aid of physical objects that represent whole numbers and cannot be calculated mentally. However, the TCM cannot explain how the indigenous children could perform the other three tasks without CWs. All three tasks required a mental representation of quantity being stored and then recalled and reproduced at a later time. The cross-modal matching task had the additional requirement of converting auditory information (i.e. four taps) into a physical representation of the same quantity. If CWs are not being used as mental placeholders to represent quantity, how are aboriginal children able to remember and replicate exact numbers across space and time?
Butterworth and Reeve (2008) conducted a follow up study to determine if a spatial recall strategy was being used to store and recall the quantities. For example, was a quantity of three counters encoded into a visual memory store in the shape of a triangle to be recalled later? They reproduced the “memory for counters” task again with a similar sample. They also manipulated the size and pattern (canonical vs. non-canonical) of the counter arrays. Again, no difference was found in task performance for indigenous and English speaking children. Across all groups, recall was higher for both smaller and canonical arrays. When assessing the method used to complete the task, the researchers found that the indigenous children used a spatial recall strategy to encode and replicate counter arrays where English speaking children were using CWs. However, the method by which the researchers deduced which strategy children used is unclear. While it is not stated explicitly, it seems logical to presume that either the children were asked which strategy they used or the researchers deduced which method was employed through observation. Both of these methods are flawed. Children may not be able to correctly articulate the process by which they complete tasks just as observers may not be able to accurately identify internal cognitive processes. Therefore this study may not give a true indication of the cognitive method used to complete the tasks. Regardless, these findings do explain how indigenous children could complete both the memory for counters and non-verbal addition tasks in the previous study; they were encoding spatial representations of the counters, (in the case of addition, manipulating them) and then reproducing them from their spatial representation. This finding however, cannot explain the indigenous children’s performance in the cross modal matching task. It is possible that as well as spatial representations of number, auditory representations of quantity (that are not CWs) can also be encoded. It follows that the indigenous children could transform these auditory representations to spatial representations and then reproduce them, using the counters.
These spatial and auditory representations of quantity cannot be readily explained by means of the TCM as it does not have a code which can process either of these (the TCM does allow for auditory input, but only in the form of CWs). It may be that these processes are omitted because the TCM was developed in cultures where CWs are the norm. Two additional elements to the TCM which would explain the interaction between spatial and auditory representations of quantity can be borrowed from Baddeley’s model of working memory (Baddeley & Hitch 1974); the visuo-spatial sketchpad and the phonological loop. These components could hold the key to explain how quantity can be encoded both spatially and audibly and, in turn, clarify how indigenous children can process an exact quantity without CWs. Instead of quantities being assigned CWs as placeholders, quantities are encoded into either the visuo-spatial sketchpad or phonological loop where they can be manipulated before exact representations are reproduced. Whether the TCM possesses its own set of dedicated components or whether it interacts with existing stores within the model of working memory would require further study to determine how quantity is encoded and transferred within the stores. I propose that both could be possible and provide a diagram of how these systems could interact (Fig ii). It is worth noting that other models of numerical processing could possibly explain the use of visual/audible encoding. Take for example the core systems model (Feigenson, Deheane & Spelke, 2004) which divides numerical processing into two cores; approximate representation of numerical magnitude and precise representations of distinct numbers. Whilst this model gives a better account of developmental numeracy than the TCM, it lacks the complexity and insight that the TCM provides in areas such as transformations of numerosity sets (Butterworth, 2010). Whilst it could allow for spatial/audible representations of numbers it is not a key feature of the model and adds little insight into cultures that do not use CWs.
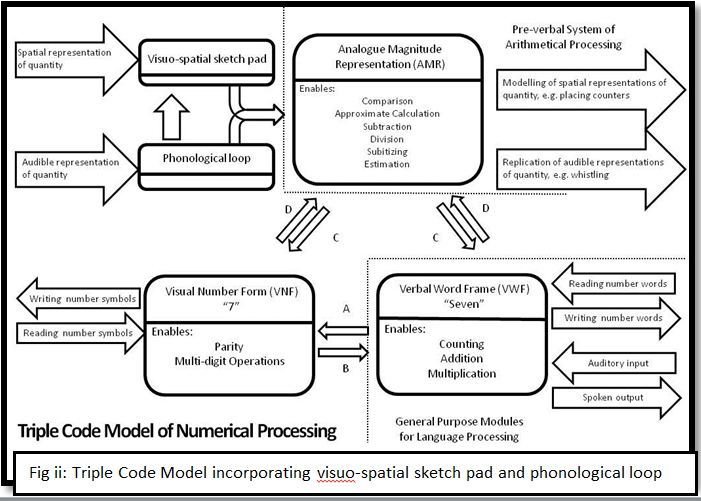
Most of the modern world tends to use the same decimal numeral system. As stated in the introduction, another important difference between cultures is the language used to represent a common numerical system. An important relationship between the VNF and the VWF within language concerns the regularity of the number system. This regularity can be deduced from examining how systematic the counting sequence of a language is and how close its written form is to its spoken form.
The English language has a relatively irregular number system. To count to 100, you not only need to know the numbers one to nine but also the meaning of every tenth number after ten; “twenty, thirty, forty” are not direct products of the words “two, three, four” and “ten”. In addition, the English number system switches the order of units throughout the counting structure. For example, take the difference in number order between thirteen (three then ten) with the order of twenty-three (‘two tens’ then three). In the case of thirteen, the order of units also has to be switched between its spoken form and its written form as thirteen reads as “three then ten” where in actuality thirteen means “ten then three”. Contrast this to a language with a regular number system such as Mandarin whereby learning the first ten numbers can enable the individual to express any number up to 100. For example “78” is spoken as “chi-shyr-ba” literally “seven-ten-eight”. A number of studies have attempted to elicit if these differences in the irregularity of number systems manifest in actual differences of mathematical ability.
The notion that Asians outperform Europeans in mathematics can be found in both scientific literature and popular culture (Ambady, Shih, Kim & Pittinsky, 2001; OECD, 2007). Not only do Asians seem to outperform Europeans in formal education, they also exhibit mathematical prowess before schooling (Suk-Han Ho & Fuson, 1998) and a number of studies imply this difference could be attributed to the corresponding regularity of the number system (Ginsberg, Lin, Ness & Seo, 2009). Tang et al. (2006) reported “remarkable differences” in brain activation between Chinese and English speakers when comparing numbers. English speakers showed higher activation in the perisylvian language area whilst Chinese speakers showed more activation in the pre-motor association area. Several studies have shown that Asian children have a much better core understanding of how numbers are formed. Fuson & Smith (1996, cited in Ho & Fuson, 1998 ) note that a significant proportion of U.S. school starters do not know that forty plus six is forty-six, they must count forward six places from forty to confirm this. Chinese children conversely would understand the equation simply from the structure of the word; “four-ten-six” (literally four tens plus six). Kamii (1985, cited in Ho & Fuson, 1998) made a similar observation in that a substantial number of U.S. first-graders believed the “1” in “16” represented “1” and not “10”. Not all studies in this field infer that the regularity of the counting system influences mathematical ability. Dowker, Bala & Lloyd (2008) examined the difference between English and Welsh (which has a regular numeracy system) speakers’ arithmetic ability and found that speakers of both languages showed similar ability. They did however find that children who spoke Welsh could compare two digit numbers more accurately than their English counterparts. It is important to note, however, that all the Welsh participants were bilingual in both languages and subsequently some may have used the English representations of the word to complete the tasks.
Miura et al. (1994) examined how children represent numbers when requested to do so with individual cubes and blocks of ten cubes. Asian children were more likely to use the blocks of ten cubes in constructing multi-digit numbers than European children. This indicates Asian children have a greater understanding of the implications of blocks of ten within the context of the decimal system. Miura et al. inferred from this that the numerical language used by a population would have a significant effect on cognitive representation of number. Saxton & Towse (1998) replicated this study and found that although Japanese children exhibited a better grasp of numerical concepts, the core knowledge that was being examined (awareness of the decimal system) was similar for both Japanese and English children. It is possible that irregularity of a number language system somehow makes it more difficult to apply existing knowledge to a task. However, without application, any knowledge is arbitrary.
The TCM would infer the work concerning the regularity of number systems is an indication that the VWF of Asian individuals allows faster encoding of visual representations of number. This is due to the fact that there is no need to reverse irregular number forms (as is required in German numerical language) or to decipher otherwise meaningless number forms (the English “Eleven” for example). These irregularities could cause interference and confusion or could effectively slow down the whole system. The simplicity of Asian number forms would mean that less cognitive resources are needed to encode numbers which may allow for faster, more complex arithmetic to take place. This could explain why Asians have been noted to possess better arithmetic skills than their European counterparts. If irregular number language restricts and slows the flow of numerical information between the three cores of numerical processing, this may manifest, not in numerical concepts being misunderstood, but in the application of these numerical concepts being slower and less accurate, as was found in Saxton & Towse (1998).
Both divisions of study concerning the effect of culture and language outlined in the introduction give rise to variation in number processing. There remains however, a large body of numerical cognition theory that has not been explored within this paper: mental number lines and the spatial-numerical-association-of-response-codes (SNARC) effect to name but two (for a full account see Göbel, Shaki & Fischer, 2011). The corpus of work examining numerical processing where number systems are fundamentally different to that of the decimal system (in particular a lack of CWs) indicates that these cultures possess less advanced arithmetic ability than that of modern cultures, although it does not impede them in their daily life. Even without CWs, concepts of quantity and exact arithmetic can be achieved using alternative techniques. Through further study, the methods by which these cultures perform numerical tasks can be incorporated into universal models of number processing. Variations in numerical processing in cultures whose number systems differ in regularity are less pronounced, although most of the evidence seems to imply a positive correlation between the regularity of the number system and mathematical ability. That is not to say that mathematical brilliance cannot be attained through an irregular number system. The TCM provides a solid framework to explore numerical processing; however this model does seem to have limited applicability in cultures whose number systems differ dramatically. The proposals in this paper for the inclusion of a visuo-spatial sketch pad and phonological loop provide a valid starting point for extending the model further to be able to explain numerical processing in cultures which do not rely on CWs in a more succinct manner.
References
AMBADY, N., SHIH, M., KIM, A., PITTINSKY, T., (2001). Stereotype Susceptibility in Children: Effects of Identity Activation on Quantitative Performance. Psychological Science, 12, (5), 385-390.
BADDELEY, A., & HITCH, G., (1974). Working memory. Psychology of Learning and Motivation, 8, 47-89.
BUTTERWORTH, B.,(2010). Foundational numerical capacities and the origins of dyscalculia. Trends in Cognitive Sciences, 14, (12), 534-541.
BUTTERWORTH, B., & REEVE, R., (2008). Verbal Counting and Spatial Strategies in Numerical Tasks: Evidence from Indigenous Australia. Philosophical Psychology, 21, 4, 443-457.
BUTTERWORTH, B., REEVE, R., REYNOLDS, F., LLOYD, D., (2008). Numerical thought with and without words: Evidence from indigenous Australian children. PNAS , 105, (35), 13179-13184.
DEHAENE, S., (1992). Varieties of numerical abilities. Cognition, 44, 1-42.
DOWKER, A., BALA, S., & LLOYD , D., (2008). Linguistic Influences on Mathematical Development: How Important Is the Transparency of the Counting System? Philosophical Psychology, 21, 4, 523-538.
DU SAUTOY, M., (2010). The Number Mysteries: A Mathematical Odyssey Through Everyday Life. London: 4th Estate.
FRANK, M., EVERETT, D., FEDORENKO, E., & GIBSON, E., (2008). Number as a cognitive technology: Evidence from Pirahã language and cognition. Cognition, 108, (3), 819-824.
FEIGENSON, L., DEHAENE, S., & SPELKE, E., (2004). Core systems of number. TRENDS in Cognitive Sciences, 8, (7), 307-314.
GINSBURG, H., LIN, C., NESS, D., & SEO, K., (2003). Young American and Chinese Children’s Everyday Mathematical Activity. Mathematical Thinking and Learning, 5, (4), 235-258.
GÖBEL, S., SHAKI, S., & FISCHER, M., (2011). The Cultural Number Line: A Review of Cultural and Linguistic Influences on the Development of Number Processing. Journal of Cross-Cultural Psychology, 42, (4), 543-565.
HO, C., & FUSON, K., (1998). Children’s knowledge of teen quantities as tens and ones: Comparisons of Chinese, British, and American kindergartners. Journal of Educational Psychology, 90, (3), 536-544.
MIURA, T., OKAMOTO, Y., KIM, C., CHANG, M., STEERE, M., & FAYOL, M., (1994). Comparisons of children’s cognitive representation of number: China, France, Japan, Korea, Sweden, and the United States. International Journal of Behavioural Development, 17, 401–411.
ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT (OECD), (2006). The Programme for International Student Assessment [online]. Retrieved 04/12/11. Available at http://www.oecd.org/dataoecd/15/13/39725224.pdf.
PICA, P., LEMER, C., DEHAENE, S., & IZARD, V., (2004). Exact and Approximate Arithmetic in an Amazonian Indigene Group. Science, 306, (5695), 499-503.
TANG, Y., ZHANG, W., CHEN, K., FENG, S., JI, Y., SHEN. J., REIMAN, E., AND LIU, Y., (2006). Arithmetic processing in the brain shaped by cultures. PNAS, 103, (28), 10775-10780.
SAXTON, M., TOWSE, J., (1998). Linguistic Relativity: The Case of Place Value in Multi-Digit Numbers. Journal of Experimental Child Psychology, 69, (1), 66-79.
WEIESE, H., (2007). The co-evolution of number concepts and counting words. Lingua, 117, (5), 758-772.