Literature Review: ‘How Do Children Learn Geometry?’

Theories of how children learn geometry have existed for centuries. Whilst some of this knowledge may still be relevant, I have chosen to focus on more recent eminent learning theories to keep my research current and up to date.

Piaget (1953; 1960; 1967) suggests that a child’s initial geometrical discoveries are topological; that they can recognise the boundary aspect of space and distinguish between open and closed figures from the age of 3. Piaget (1953) suggests this development seems to be formulated during the latter sub-stages (tertiary, circular reactions, curiously and novelty) of the formative sensorimotor stage when a child interacts with the world around them and begins to explore the properties of new objects. Bruner (1961), a critic of Piagetian theory, reaffirms this by proposing that children learn by exploring their surroundings and physical environment.

However, Bruner (1961) places more importance on social learning than Piaget and implies that children learn in a social constructivist model from More Knowledgeable Others (MKOs) and their peers (Vygotsky 1962; 1978). This seems to be an underlying criticism of Piaget’s method: that he fails to recognise the social aspect of learning. French (2004) goes further in their criticisms of Piagetian theory by stating that his experiments were not appropriate and that children did not understand what the tasks required to them to do. Hughes (1986) supports this and also states that due to the arrangements of the task children were limited to egocentricity and could not see another viewpoint. However, Glasserfeld (1995) refutes these criticisms and attributes the children’s lack of understanding to the conceptual difference of the mistranslated Piaget text. Regardless of the agreement of the various cognition theories, there seems to be some truth that children learn Geometry in a social aspect. DfE (2012) state this is noticeably prominent when a child starts formal education and learns from teacher exposition and interaction with their peers.

A child’s formative study of Geometry in school is quite heavily centred towards Euclidean Geometry which consists of understanding the patterns and properties of shape (DfE, 2012). Both Piaget (1967) and Bruner (1961) allude to the concept of prototypical images, where an image of a shape is constructed in a child’s mind and stored for later use, although both describe it in different ways. Dadds (2009) state this learning style could be fostered if there was a significant amount of teacher exposition and board work in lessons, particularly in topics such as measures and mensuration. Piaget (1953) theorised that children have symbolic schemata which are mental pictures or images or what they have experienced in lessons. Bruner (1966) described this method of remembering images as iconic.

Van Hiele (1985) as cited in French (2004, p.15) defines a model of geometric levels that children progress through:

• Level 1 (Visualisation) – Children have knowledge of basic shapes but no knowledge of their properties. Cannot link or compare shapes.
• Level 2 (Analysis) – Children understand the properties of shapes but do not compare shapes using them.
• Level 3 (Abstraction) – Children can make links between shapes based on their properties and can understand some very simple proofs although they may struggle on more formal examples.
• Level 4 (Deduction) – Children have a good knowledge of Geometry and can use and apply some formal proofs. Children are likely to reach this level at the end of secondary school.
• Level 5 (Rigor) – This is a level of geometric understanding equivalent to that of a Mathematician and is unlikely to be reached in compulsory education. People at this level have a deep knowledge of formal proofs and can work confidently in most areas of Geometry.

Van Hiele (1985) states a child’s initial study of Geometry at school is the visualisation level (Level 1 in his model), where children have a simple understanding of basic geometrical figures like shapes, but no knowledge of their interrelating properties.

However, DfE (2012) state that children are taught to make connections between shapes from KS1. This seems to imply that children will have some knowledge of the connectionist properties of Euclidean Geometry; in a Piagetian sense by linking it back to previous schemata and also by using visual prototypes to identify other shapes in the Van Hiele model. Mitchelmore and Outhred (2004) observed that this is often done in comparison with everyday objects; for example, a rectangle is formed in the mind because it looks like a box. It could be conjectured that this formative geometric reasoning is normally only applied to Euclidean spaces (shapes or figures which a defined by a set of axioms or postulates) in the school environment but can be applied to other spaces outside of this. Furthermore, the Van Hiele model (1985) does not acknowledge that children learn in a number of different ways; Baume and Fleming (2006) suggest children mostly learn through Visual, Audio, Reading and Kinaesthetic (VARK) methods. This, and the success of using multi-sensory approaches in teaching to respond to these needs, may influence the rate of progression in children’s geometrical knowledge.

At primary school level, the teaching strategies used are often a mixture of inductive (practical investigations and kinaesthetic activities) and deductive (formal teaching and exposition) which constitute the first stage of Geometry teaching (French, 2004, p.54). There does seem to be evidence that children are more influenced by deductive teaching particularly in their approach to prototypical images.

Kerslake (1979) investigated whether primary-school-aged children could recognise angles and shapes of different orientations and found that most only correctly identified the ‘typical’ image (the orientation of angle/shape that was normally drawn by their class teacher) whereas ‘unfamiliar’ images were not recognised. Burger (1986) rationalises this as younger children often believing a rule based on one example, normally from the class teacher and are unable to extrapolate this to other shapes.

This research seems to validate Piaget’s assertion that at this stage children view figures holistically without any realisation of their properties. However, children who have natural ability in Geometry, normally those with a pre-disposition to the right cerebral hemisphere (OECD, 2002), may not be categorised by this developmental model, although current research has concerns over the validity of this model (Carter, 2004). Another possible flaw in Piaget’s theory is that the levels are classified by stages where subjects are at an approximate age: progression in Geometry is not necessarily linear. The seemingly more flexible Van Hiele Model (1985) may be a better indicator of assessing a child’s progress in Geometry as it is based on instruction and experience rather than age.

Upon learning about angles and lines, children may be able to make better links between shapes. Van Hiele (1985) termed this level as analysis where pupils could understand the properties of shape but not yet link them. Piaget (1967) and Bruner (1961) both support this in their respective pre-operational stage and symbolic models, although Bruner recognises that these seemingly autonomous mental structures can be blended together and related depending on the age and experience of the child. This model is in sharp contrast to Piaget’s age-centric theory; Bruner philosophises that a child can learn any task given the right teaching. Again, perhaps due to the abundance of command, teacher-led strategies (Mosston, 1966) pupils may develop an inflexible arbitrary knowledge of Geometry which can be a barrier to progression (Hewitt, 1999). Some students particularly struggle with angle and cannot quantify or grasp the ‘big idea’ that it is a measure of turn (Ofsted 2008; 2012).

Strategies to overcome this could include having more varied examples of a shape’s orientation and for the teacher to develop a connectionist orientation and make more links between topics. Teachers could also try to promote higher-order thinking by encouraging children to analyse what they have learnt, although the process of carefully examining what they have been taught may be too complex for children to grasp when studying primary school level mathematics and may have to be handled with care (Ofsted, 2011).

Once children have grasped the basic notions of angle and shapes, they can begin to make links between them. At the Piagetian concrete operations stage, a child can think logically and solve problems which are heavily generalised and require an inductive manner of thinking. This is perhaps comparable to GCSE exams where children are generally able to competently solve ‘method’ questions but sometimes struggle with ‘worded’ or ‘applied’ problems (Ofsted, 2012). This obstacle to progression in Geometry at this level is perhaps explained by the heavy influence of Euclidean Geometry on the Primary and Secondary Mathematics curriculum (DfE 2013). This could possibly be rectified by introducing non-Euclidean geometries such as elliptic geometry. Children are unlikely to have mastered 3-Dimensional thinking at this level and may not have encountered plane geometry, this may not be advisable.

Roughly when a child starts secondary school, they enter the Van Hiele abstraction stage where they can compare shapes and make connections such as in the diagram below:

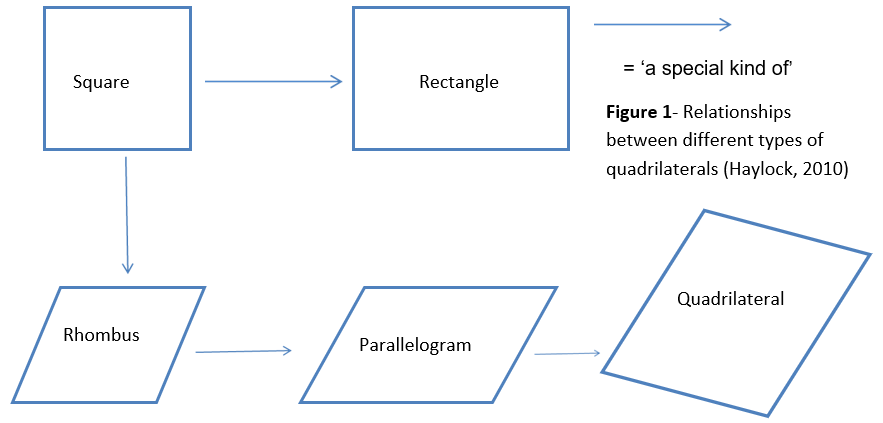
The progression to the child thinking in a slightly more abstract manner and the knowledge of the properties of 2-D shapes may help a child to understand plane geometry and that of 3-D polyhedra and platonic solids such as cubes and tetrahedrons. A knowledge of Euclidean Geometry and a developing knowledge of spatial awareness (through studying topics like tessellations) is conducive to understanding affine geometry, the study of parallel lines which is introduced in Mathematics at KS3 Level (DfE, 2013).

The progressive and interrelating nature of Geometry seems to be further represented by the fact that knowledge of affine geometry can help with understanding of the beginnings of co-ordinate and graphical geometry in Secondary School in modules like transformations (DfE, 2013). It may also be beneficial to study vector geometry both at secondary school (translations) and A-Level (magnitude, direction, scalar product and equation of a vector).

However, Haggerty (2001) asserts not all geometrical learning is linear and discrete; it can be discontinuous as pupils develop at different rates. Many pupils develop misconceptions on plane geometry and require technology support packages such as LOGO and Cabri which can be transferred to paper so pupils can learn in an enactive manner (Bruner, 1961; French, 2004; Johnston-Wilder and Mason, 2005). A possible criticism of the Piagetian and Van Hiele models is that they are heavily generalised and do not account for variations in ability. Furthermore, Piaget’s model is domain specific and surmises that cognitive development is homogenous across all fields which may not be true; as the OECD (2008) emphasise distinction between pure and applied mathematicians implies.

It seems that a clear understanding of all the fields of Geometry is needed before a child can develop deductive logic and understand formal Euclidean proofs such as proving there are 180 degrees in a triangle and congruency. Piaget (1953) argues that children do not enter the formal operational stage until they are 14 and that they are not cannot learn formal proofs before this period. Van Hiele (1985) describes similar properties in his penultimate geometric level deduction although he does not specify which age pupils reach this level. This seems to be supported by the curriculum as proofs are not normally covered until Year 10 although some students study it in Year 9 in accelerated study programs (DfE, 2011). DfE (2011) highlights concerns that, in many cases pupils do not reach this level due to the perceived ‘test-teaching’ nature of proofs in school; formulas and rules are often learnt by rote with no understanding of the mathematics behind them: for example the hypotenuse of a right-angled triangle used in Pythagoras’ Theorem is typically learnt as an arbitrary concept ‘c’ rather than a necessary fact that it is ‘always opposite the right angle’.

A supposition could be presumed that all students need a good comprehension of Algebra to comprehend more sophisticated Geometry topics. This seems to be evidenced by curriculum content; GCSE and A Level Mathematics contain more Algebraic Geometry and a reduced amount of Euclidean Geometry. Indeed, Geometry in A Level Mathematics is almost exclusively made up of Co-ordinate and Differential Geometry (Calculus) and some Trigonometry with barely any pure, Euclidean Geometry. Parliament (2012) and Ofqual (2012) perceive this to be a weakness of the course, which could stop pupils reaching the final Van Hiele (1985) level of rigour, where a pupil has mastered all the axiomatic structures of Geometry and can confidently deal with Non-Euclidean Geometries.

In conclusion, a broad (and not necessarily linear) generalisation of the way in which children learn geometrical concepts seems to concur with the fields of Geometry in reverse chronological order in which they were discovered. The Euclidean axiomatic system (and formal proofs) was the first area of Geometry to be discovered over 2,000 years ago whereas projective geometry was invented around the 17^th century and finally topological geometry was formulated in approximately the 19^th century (Piaget, 1953). In learning Geometry, pupils seem to develop from pure and synthetic geometry (Euclidean) but need to have an understanding of Algebra to attain more sophisticated levels of analytic (Algebraic Geometry). It could be suggested that there is a finite level of a geometrical reasoning that a student and that their understanding of geometry will eventually plateau.

The literature seems to suggest that determining whether the Van Hiele Model is appropriate in assessing children’s geometrical abilities is something which needs to be examined. The potential impact of knowledge of the Van Hiele model may have on teaching and learning also seems to be a relevant issue to be considered.

Reference List

• Baume, D. and Fleming, N. (2006) ‘Learning Styles Again: VARKing up the right tree!’ Educational Developments, 7 (4), pp. 4-7.
• Bruner, J. S. (1961). The act of discovery. Harvard Educational Review, 31, 21-32.
• Burger, S. (1986) ‘Characterizing the Van Hiele Levels of Development in Geometry.’ Journal for Research in Mathematics Education, 17 (1), pp. 31– 48.
• Carter, R. (2004) Mapping the Mind. London: Phoenix.
• Dadds, M. (2009) From Passionate Enquiry to Loving Detachment. The Sage Handbook of Educational Action Research. Los Angeles: Sage.
• French, D. (2004) Teaching and Learning Geometry. London: Continuum.
• Glasersfeld, E. (1995) Radical Constructivism: A way of Knowing and learning. London: Routledge Falmer.
• Great Britain. Department for Education (2012) Schools’ White Paper: The Importance of Teaching. London: DfE.
• Great Britain. Department for Education (2013) Secondary Mathematics Curriculum until 2014. [Online]. Available at: https://www.education.gov.uk/schools/teachingandlearning/curriculum/secondary/b00199003/mathematics (Accessed: 28 May 2013).
• Great Britain. Ofsted (2008) Mathematics: Understanding the score. London: Ofsted.
• Great Britain. Ofsted (2012 b) Mathematics: Made to Measure. London: Ofsted.
• Great Britain. Ofsted (2012) Every pupil needs a good mathematics education. London: Ofsted.
• Haggerty, L. (2001) Aspects of teaching Secondary Mathematics. London: Routledge Falmer.
• Haylock, D. (2010) Mathematics Explained for Primary Teachers. Los Angeles: Sage.
• Hewitt, D. (1999) ‘Arbitrary and necessary Part 1: a way of viewing the Mathematics Curriculum.’ Learning of Mathematics, 19: 3.
• Hughes, M. (1986) Children and Number: Difficulties in Learning Mathematics. London: Basil Blackwell.
• Johnston-Wilder, S. and Mason, J. (2005) Developing thinking in Geometry. London: Sage.
• Kerslake, D. (1979) ‘Visual Mathematics.’ Mathematics in School, 8, 2, pp. 34-35.
• Mitchelmore, M. and Outhred, L. (2004) ‘Students’ structuring of rectangular arrays.’ Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 3, pp. 465-472.
• Mosston, M. (1966) Teaching Physical education. Ohio: Merrill.
• Ofqual (2012) Fit for Purpose? The view of the higher education sector, teachers and employers on the suitability of A levels.
• Organisation for Economic Co-operation and Development (2008) Report on Mathematics in Industry. [Online]. Available at: http://www.oecd.org/science/sci-tech/41019441.pdf (Accessed: 2 August 2013).
• Parliament (2012) Higher Education in Science, Technology, Engineering and Mathematics (STEM) subjects – Science and Technology Committee. [Online]. Available at: http://www.publications.parliament.uk/pa/ld201213/ldselect/ldsctech/37/ 3702.htm (Accessed: 2 August 2012).
• Piaget, J. (1953) ‘How Children Form Mathematical Concepts’. Scientific American.
• Piaget, J. (1960) Child’s Conception of Geometry. New York: Basic Books.
• Piaget, J. (1967) The Child’s Conception of Space. New York: W.W. Norton.
• Van Hiele, P. (1985) The Child’s Thought and Geometry. Brooklyn, NY: City University of New York.
• Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Cambridge, MA: Harvard University Press.
• Vygotsky, L.S. (1962). Thought and Language. Cambridge MA: MIT Press.